Research
I have been involved in atomic and electronic structure calculations, developing and employing various state-of-art packages based on the formulations such as Density Functional Theory, Hartree Fock Theory, Configuration Interaction method and Solvation techniques throughout my research career.
Below are the details of various ongoing as well as past projects. Click on the titles to know more.
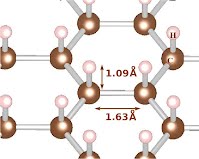
New theory for Magnetism in Random Alloys
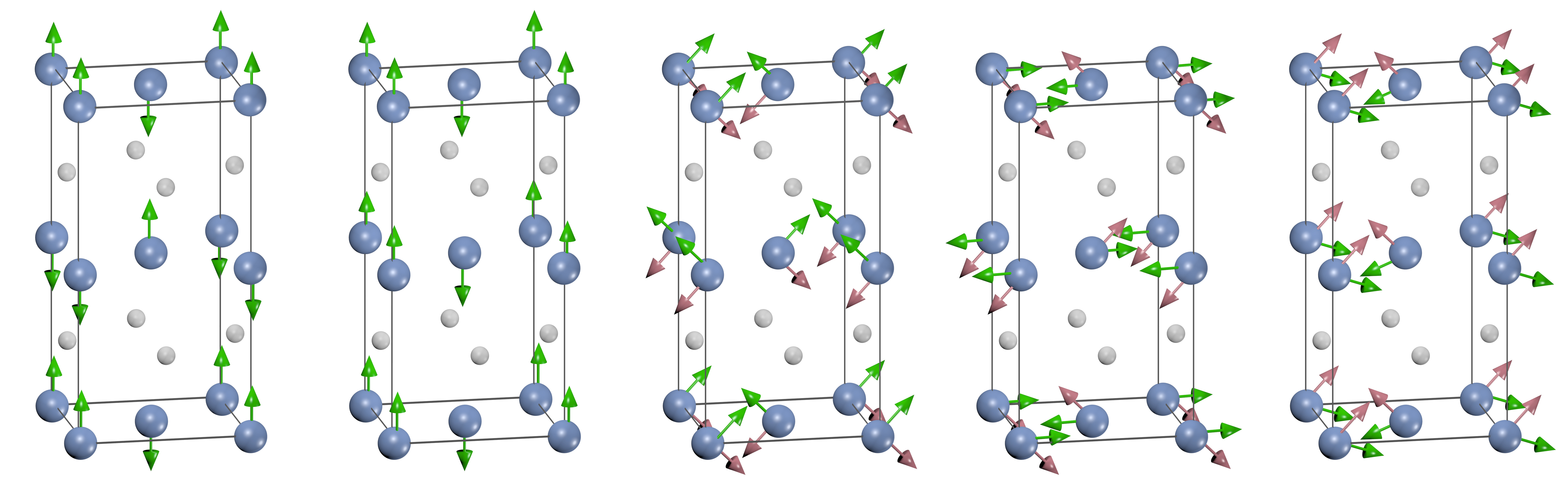 The Fe1-xMnxPt system exhibits five
magnetic structures, including a ferromagnetic phase, two
antiferromagnetic phases, and two noncollinear ones [1]. The
latter are characterized by superpositions of orthogonal magnetic
amplitudes at two commensurate magnetic wave vectors. Here we
study the magnetic interaction in this system and construct the
magnetic phase diagram based on total energy calculations within
the vector-DLM (disordered local moment) method representing
partially ordered magnetic states in the coherent potential
approximation (CPA). This method has been implemented within the
linear muffin-tin orbital basis. The calculated total energies
are fitted to polynomial functions of the relevant order
parameters (magnetization amplitudes at the relevant wave vectors
for the two components), which are subsequently used to evaluate
the free energy in the mean-field approximation. The interaction
between spatially orthogonal amplitudes is evaluated by
noncollinear total energy calculations for representative alloy
configurations. The phase diagram is constructed by minimizing
the free energy at each concentration and temperature. The
structure of the resulting phase diagram agrees with neutron
diffraction measurements, demonstrating the applicability of the
method to the studies of magnetic phase diagrams of intermetallic
alloys with competing ferromagnetic and antiferromagnetic
interactions.
The Fe1-xMnxPt system exhibits five
magnetic structures, including a ferromagnetic phase, two
antiferromagnetic phases, and two noncollinear ones [1]. The
latter are characterized by superpositions of orthogonal magnetic
amplitudes at two commensurate magnetic wave vectors. Here we
study the magnetic interaction in this system and construct the
magnetic phase diagram based on total energy calculations within
the vector-DLM (disordered local moment) method representing
partially ordered magnetic states in the coherent potential
approximation (CPA). This method has been implemented within the
linear muffin-tin orbital basis. The calculated total energies
are fitted to polynomial functions of the relevant order
parameters (magnetization amplitudes at the relevant wave vectors
for the two components), which are subsequently used to evaluate
the free energy in the mean-field approximation. The interaction
between spatially orthogonal amplitudes is evaluated by
noncollinear total energy calculations for representative alloy
configurations. The phase diagram is constructed by minimizing
the free energy at each concentration and temperature. The
structure of the resulting phase diagram agrees with neutron
diffraction measurements, demonstrating the applicability of the
method to the studies of magnetic phase diagrams of intermetallic
alloys with competing ferromagnetic and antiferromagnetic
interactions. [1] A. Z. Menshikov et al., J. Magn. Magn. Mater. 65, 159 (1987).
Published in : Phys. Rev. Lett. 115, 057203 (2015)
Graphene and its derivatives
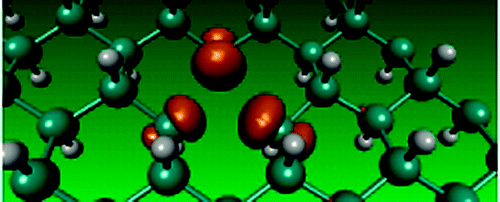
In the latest density functional study, we demonstrate that single-side-hydrogenated graphene (termed as SSHGraphene) is a semiconductor with an indirect band gap of 1.35 eV, which is in between the gapless graph ene and wide band-gap graphane and surprisingly close to silicon. We show that its electronic structure and lattice characteristics are substantially different from those of graphene, graphone, or graphane. The lattice parameter and C-C bond length are found to be lengthened by 15% of those of graphene. Our binding-energy analysis confirms that such a single-sided hydrogenation leads to energetically stable material, making it a promising candidate as an organic semiconductor.
Phys. Rev. B 84, 041402(R) (2011) (Rapid Communications)
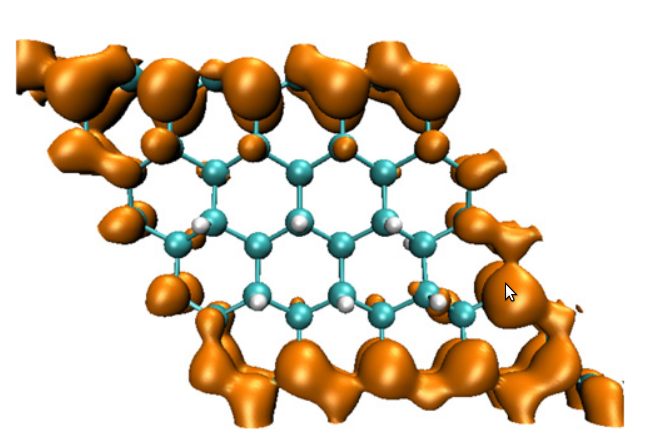 Earlier, we have probed the transformation of
graphene upon hydrogenation to graphane within the
framework of density functional theory. By analysing
the electronic structure for 18 different hydrogen
concentrations, we brought out some novel features of
this transition. Our results showed that the
hydrogenation favored clustered configurations
leading to the formation of compact islands. The
analysis of the charge densities and electron
localization functions (ELF) indicated that, as
hydrogen coverage increases, the semi-metal turns
into a metal, (showing a delocalized charge density,)
then transforms into an insulator. The metallic phase
was spatially inhomogeneous in the sense it contained
islands of insulating regions formed by hydrogenated
carbon atoms and metallic channels formed by
contiguous bare carbon atoms. It turned out that it
is possible to pattern the graphene sheet to tune the
electronic structure. For example, removal of
hydrogen atoms along the diagonal of the unit cell,
yielding an armchair pattern at the edge, gave rise
to a bandgap of 1.4 eV. We also showed that a weak
ferromagnetic state exists even for a large hydrogen
coverage whenever there was a sublattice imbalance in
the presence of an odd number of hydrogen atoms.
Earlier, we have probed the transformation of
graphene upon hydrogenation to graphane within the
framework of density functional theory. By analysing
the electronic structure for 18 different hydrogen
concentrations, we brought out some novel features of
this transition. Our results showed that the
hydrogenation favored clustered configurations
leading to the formation of compact islands. The
analysis of the charge densities and electron
localization functions (ELF) indicated that, as
hydrogen coverage increases, the semi-metal turns
into a metal, (showing a delocalized charge density,)
then transforms into an insulator. The metallic phase
was spatially inhomogeneous in the sense it contained
islands of insulating regions formed by hydrogenated
carbon atoms and metallic channels formed by
contiguous bare carbon atoms. It turned out that it
is possible to pattern the graphene sheet to tune the
electronic structure. For example, removal of
hydrogen atoms along the diagonal of the unit cell,
yielding an armchair pattern at the edge, gave rise
to a bandgap of 1.4 eV. We also showed that a weak
ferromagnetic state exists even for a large hydrogen
coverage whenever there was a sublattice imbalance in
the presence of an odd number of hydrogen atoms. J. Phys.: Condens. Matter 22 465502,(2010)
This work is featured in “IOP Select November-2010”
In first problem we carried out ab initio electronic structure calculations on graphane having single
and double vacancy defects. Our analysis of the density of states reveals that such vacancies induce the mid-gap states and modify the band gap. The induced states are due to the unpaired electrons on carbon atoms surrounding the vacancy. Interestingly, the placement and the number of such states is found to be sensitive to the distance between the vacancies. It turns out that such vacancies also induce a local magnetic moment.Proton hopping in Organometallic complex
 Using ab-inito molecular dynamics as well as Nudge Elastic Band simulations we examine the transfer of proton across a complex Organometallic compound. The compound synthesized by the experimental group at the Department of Chemistry shows the promising conductivity as a function of humidity. With the aid of ab-initio calculations we compute the activation energy along with the electronic structure calculations. The theoretical as well as computational results are in excellent agreement with each other.
Using ab-inito molecular dynamics as well as Nudge Elastic Band simulations we examine the transfer of proton across a complex Organometallic compound. The compound synthesized by the experimental group at the Department of Chemistry shows the promising conductivity as a function of humidity. With the aid of ab-initio calculations we compute the activation energy along with the electronic structure calculations. The theoretical as well as computational results are in excellent agreement with each other.
Paper in communication
Materials under extreme conditions
Ab-initio studies of Ferroelectric materials
Lead zirconate titanate (PZT), a ceramic perovskite material is used as a component in ultra- sound transducers, ceramic capacitors, STM/AFM actuators, FRAM chips and sensors. PZT has also been used in the manufacture of ceramic resonators for reference timing in electronic circuitry. PZT is usually not used in its pure form but doped with either acceptors to create anion vacancies or with donors to create cation vacancies. Acceptor doping creates hard PZT and donor doping creates soft PZT, which are differentiated based on their piezoelectric constants. These piezoelectric constants are proportional to the polarization i.e. the electric field generated per unit of mechanical stress. Usually soft PZT has a higher piezoelectric constant but larger losses in material whereas hard PZT has lower piezoelectric constant and lower losses in material. With this view, we are interested in performing first principles density functional theory (DFT) based calculations on undoped and doped PZT materials.
Solvation
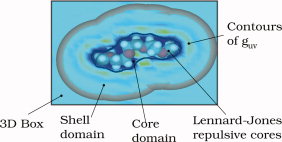
We developed a technique to decrease memory requirements when solving the integral equations of three-dimensional (3D) molecular theory of solvation, a.k.a. 3D reference interaction site model (3D-RISM), using the modified direct inversion in the iterative subspace (MDIIS) numerical method of generalized minimal residual type. The latter provides robust convergence, in particular, for charged systems and electrolyte solutions with strong associative effects for which damped iterations do not converge. The MDIIS solver (typically, with 2 × 10 iterative vectors of argument and residual for fast convergence) treats the solute excluded volume (core), while handling the solvation shells in the 3D box with two vectors coupled with MDIIS iteratively and incorporating the electrostatic asymptotics outside the box analytically. For solvated systems from small to large macromolecules and solid–liquid interfaces, this results in 6- to 16-fold memory reduction and corresponding CPU load decrease in MDIIS. We illustrated the new technique on solvated systems of chemical and biomolecular relevance with different dimensionality, both in ambient water and aqueous electrolyte solution, by solving the 3D-RISM equations with the Kovalenko–Hirata (KH) closure, and the hypernetted chain (HNC) closure where convergent. This core–shell-asymptotics technique coupling MDIIS for the excluded volume core with iteration of the solvation shells converges as efficiently as MDIIS for the whole 3D box and yields the solvation structure and thermodynamics without loss of accuracy. Although being of benefit for solutes of any size, this memory reduction becomes critical in 3D-RISM calculations for large solvated systems, such as macromolecules in solution with ions, ligands, and other cofactors.
Journal of Computational Chemistry Volume 33, Issue 17, pages 1478–1494, 30 June 2012